Площадь параллелограмма

Геометрия — один из наиболее сложных разделов школьного курса математики. Причина такой сложности состоит в том, что для решения геометрических задач часто требуются нестандартные подходы и пространственное мышление.

При это очень мало стандартных алгоритмов, к которым привыкли школьники. Приходится думать с опорой на теоретический багаж, причем довольно простые формулы часто не приходят ученику в голову там, где должны автоматически всплывать подсказки.

Одной из таких формул является выражение для определения площади параллелограмма, о которой и пойдет речь в этой статье.

Площадь параллелограмма — сколько их?

Площадь геометрических фигур издавна интересовала людей, как прикладной объект. Уже древние египтяне были довольно хороши в соответствующих подсчетах, потому что их вынуждала окружающая действительность.

Землемеры и сборщики налогов интересовались площадями не для решения школьных задач и не для получения высокого балла на ЕГЭ. Их интерес был более приземленным:

• землемеры стремились усовершенствовать методы разметки сложных участков земли под сельскохозяйственные и строительные нужды;
• сборщики податей хотели знать, сколько должен «налогоплательщик».

Эти простые вопросы приблизили человечество к современной науке и те сложные понятия, которыми оперируют математики, до сих пор базируются на простых формулах. В этом ряду площадь параллелограмма занимает особенное место, потому что это универсальная геометрическая фигура, частными случаями которой являются:

• прямоугольник;
• квадрат;
• ромб.

Даже треугольник — просто половина параллелограмма, что делает операции с этой фигурой важной частью базовых знаний. Давайте вспомним ее основные свойства:

• противоположные стороны параллельны;
• противолежащие углы попарно равны;
• сумма прилежащих углов равна 180°;
• диагонали и средние линии пересекаются в одной точке, которая делит их пополам.

С параллелограммом связано несколько интересных формул и работа с площадями — в их числе. Этот параметр можно найти несколькими способами, которые мы подробно изучим ниже с примерами.

Площадь параллелограмма по стороне и высоте

У нас есть параллелограмм АВСD, из вершины которого на противоположную сторону опущена высота ВН, пересекающая АD под прямым углом. Площадь фигуры АВСD равна произведению стороны АD на ВН.

• S _АВСD = АD x ВН.

Пример 1. Дан параллелограмм АВСD, площадью которого считается 50 см², а сторона СD — 5 см. Найти высоту ВЕ, опущенную на сторону СD из вершины В.

Решение

Запишем выражение для нахождения площади:

• S _АВСD = СD x ВЕ.

Выразим из нее ВЕ и подставим значения из условия:

• ВЕ = S _АВСD / СD = 50 / 5 = 10 см.

Ответ: ВЕ = 10 см.

Площадь параллелограмма по сторонам и углу между ними

Формулировка: площадь параллелограмма равна произведению двух сторон параллелограмма на синус угла между ними.

• S _АВСD = AB x AD х sin ∠BAD = AB x AD х sin ∠ABC.

Пример 2. Найти сторону ромба, если один из его углов равен 30 градусов, а S — 50 см².

Решение

Поскольку ромб — это частный случай параллелограмма, воспользуемся соответствующей формулой:

• S _АВСD = AB x AD х sin ∠BAD.

В этом уравнении нам известны данные площади и угла. Поскольку стороны ромба равны, то преобразуем выражение следующим образом:

• AB x AD = S _АВСD / sin ∠BAD,
• AB² = S _АВСD / sin ∠BAD.

Подставим значения из условия:

• AB² = 50 / sin 30°.

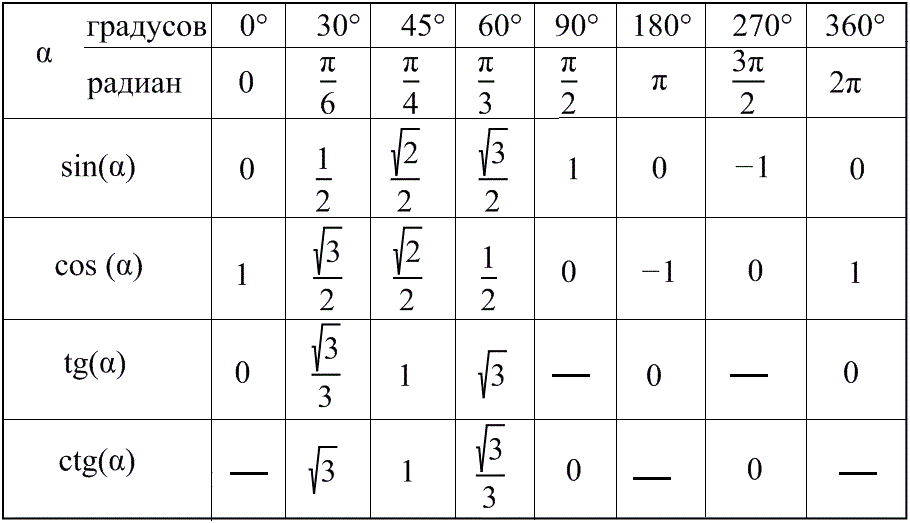
Значение синуса посчитаем на калькуляторе, выберем из таблицы Брадиса (для тех, кто помнит этого прекрасного человека) или из представленной в этой статье таблицы. В итоге выражение преобразуется следующим образом:

• AB² = 50 / 0,5 = 100.

Выразим из этого выражения АВ:

• AB = √100 = 10 см.

Ответ: AB = 10 см.

Площадь параллелограмма по диагоналям и углу между ними

Формулировка: площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

• S _АВСD = ½ AС x ВD х sin ∠BОС = ½ AС x ВD х sin ∠BОА

Пример 3. Дан параллелограмм АВСD, диагонали которого равны по 20 см, а угол между ними составляет 90 градусов. Найти площадь треугольника АВD.

Решение

Заметим, что площадь треугольника АВD, который образуется путем деления параллелограмма АВСD его диагональю АD составляет половину площади самого параллелограмма. Это следует из равенства треугольников АВD и АСD по трем сторонам:

• сторона АВ равна стороне СD,
• сторона ВС равна стороне АD,
• сторона ВD общая.

Запомним это и перейдем к поискам площади параллелограмма:

• S _АВСD = ½ AС x ВD х sin ∠BОС.

Подставим в эту формулу значения из условия:

• S _АВСD = ½ х 20 x 20 х sin 90°.

Значение синуса выберем из предыдущей таблицы:

• S _АВСD = ½ х 20 x 20 х 1 = ½ х 400 = 200 см².

Вспомним, что площадью треугольника АВD называется половина площади самого параллелограмма, то есть 100 см². Надеемся, внимательные читатели заметили, что наш параллелограмм с равными диагоналями, пересекающимся под прямым углом — это квадрат.

Ответ: S треугольника АВD — 100 см².

Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Остались вопросы? Задайте их эксперту!

Владислав Барышников

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР

Задать вопрос

Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.